量化专题：隐马尔可夫模型商品期货应用初探

报告摘要

本报告主要介绍了隐马尔可夫模型的基本概念、模型及相关问题。并简单选取了一些技术分析指标纳入模型的可观察向量中，根据模型给出的结果对螺纹钢主力合约进行价格预测。

隐马尔可夫模型（HMM）被用来描述一个含有隐含未知参数的马尔可夫过程，它的状态不能直接观察到，但能通过可观察向量序列观察到。

将适当的技术指标纳入隐马尔可夫模型可观察向量组来预测螺纹钢期货的后期走势能取得一定的效果。但由于隐马尔可夫模型每次运行所得的隐状态分类较为随机，上升隐状态和下降隐状态是根据收益曲线人工区分而来的，模型的稳定性还有待提升。

一、隐马尔可夫模型介绍

1.1 马尔可夫过程

马尔可夫过程（Markov Process），安德烈·马尔可夫于1906年最早定义了这样的一个随机过程，并模拟生成了一条状态序列，该状态序列在任一时刻的预期状态都只与上一时刻的状态信息有关，这一特征被称为马尔科夫性质。在该过程中，每个状态的转移只依赖于在此之前的n个状态，这个过程被称为1个n阶的模型，其中n是影响转移状态的数目。一阶马尔可夫过程是最简单的马尔可夫过程，任何时刻的状态的转移只依赖于其前一时刻的那一个状态。值得注意的是，这一过程与确定性过程有明显差异，状态之间的转移不是确定性的，而是有一定概率的。

这里x为过程中的某个状态。上面这个恒等式可以被看作是马尔可夫性质。例如，假设某地只存晴天、阴天和下雨天三种天气，某一天该地的天气状况的概率只与前一天的天气状况有关，而与之前过去所有日子的天气状况无关，那么这个天气变化的随机过程就是一个马尔科夫过程。

在上面的例子中，定义了以下三个部分：状态：晴天、阴天和下雨天；初始向量为：定义系统在时间为0的时候的状态的概率；状态转移矩阵：不同天气之间转换的概率都能被这样描述的系统就被称为一个马尔可夫过程

但是，在某些特定的情况下，简单的马尔可夫过程并不能描述我们想要发现的模式。例如，假设某个整天在屋子里的盲人并不能观察到今天外面的天气情况，但是屋内植物的状态在某种概率上是和外面的天气情况相关的。在这样的情况下，我们有两个不同的状态序列，一个是可以被观察到的状态序列（屋内植物的状态），还有一个是观察不到的隐藏状态序列（外面的天气情况），我们希望可以找到一种算法来根据马尔可夫过程和屋内植物的状态来预测外面的天气情况。

在上面的这种情况，可以观察到的状态序列和隐藏的状态序列在一定程度上是概率相关的。于是我们可以将这种情况的过程描述为一个可以被观察到的序列以及和观察序列概率相关的一个隐藏状态序列的马尔可夫过程。这就是接下来要介绍的隐马尔可夫模型。

1.2 隐马尔可夫模型

隐马尔可夫模型本质上是基于马尔可夫过程衍生出的一种概率图模型，他被用来描述一个含有隐含未知参数的马尔可夫过程，该模型假设一组可观察序列是由一些隐藏的状态生成，这些隐状态的转移过程是一个马尔科夫过程，每一个隐状态对应一个或几个可观测到的变量。通常隐状态的转移概率矩阵未知，观测序列是由哪个隐状态序列生成也是未知的，需要通过观测值序列作为隐马尔科夫模型的输入变量来推测。

除了上面植物与天气的例子，还可以用一个比较直观的例子来表述隐马尔可夫模型。假设一个房间里面有三个不同的箱子，编号分别为1，2，3，每个箱子里都装有个数不同的红黄蓝三种颜色的球，有一个盲人每次从其中的一个箱子里摸出一个球，然后将摸出的球丢出房间，房间外面的人会记录球的颜色，再让盲人把球放回原来的箱子。虽然在整个过程中，盲人并不清除他丢出去的球是什么颜色，但他通过箱子的形状可以知道摸的球来自其中哪个箱子，而且他选择箱子的行为是一个离散马尔可夫链。这样在盲人进行多次扔球后，房间外面的人知道每次扔出来的球颜色的序列，还清楚房间里面有几个箱子，但是不了解盲人选择箱子的规律(也就是被隐藏起来的马尔可夫链)和不同箱子里面不同颜色球的分布。这就是一个离散的隐马尔科夫模型。

下图是一个由三个状态组成的隐马尔可夫模型的状态转移图，其中Q 表示隐含状态，O表示可观察的序列，a表示状态转换概率，b 表示输出概率。

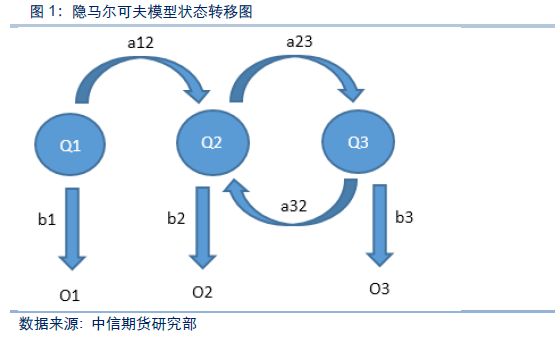
1.3 隐马尔可夫模型的三个典型问题

不管在什么领域，如果使用隐马尔可夫模型来进行模式识别，通常会遇到以下三个问题：

给定一个HMM模型，计算生成给定可观察序列的概率——评估问题

已知生成的可观察序列，如何得到最可能的隐藏状态序列——解码问题

已知可观察序列，如何得到一个最优的模型参数——学习问题

这就是隐马尔可夫模型的三个典型问题。

1.3.1 评估问题

1.3.2 解码问题

1.3.3 学习问题

二、HMM模型商品期货市场应用

2.1 技术指标以及时间段选取

我们选取的时间段为2010年1月1日至2018年2月14日，共1976个交易日，数据来源于Wind。数据选取螺纹钢期货主力合约的价格以及成交量数据，因为商品期货同股票市场有较大差别，同一时间同一商品会有多个合约进行交易。我们只选取当前的主力合约进行分析，主力合约即当前持仓量最大的合约，随着时间的推移，主力合约会在不同月份合约之间转换。为了避免合约换月带来的价格跳跃，我们在计算收益率时，合约换月当天仍采用次主力合约的数据进行计算。

我们将数据分为两部分，进行模型外预测。使用2010年1月1日至2016年11月25日，共1676个交易日的数据建立HMM模型。通过建立的模型对2016年11月28日至2018年2月14日共300个交易日的数据进行预测分析，建立交易策略。

价格与成交量的变化能较好的反应当前金融产品的状态信息。技术指标方面，我们选取一日对数成交量差、五日对数成交量差、一日对数收盘价差、五日对数收盘价差以及当日对数高低价差等5个指标作为可观察序列带入到本报告的HMM模型中进行分析。五个指标的介绍如所示：

一日对数成交量差＝log（当日成交量）-log（上一交易日成交量）

五日对数成交量差＝log（当日成交量）-log（五日前成交量）

一日对数收盘价差＝log（当日收盘价）-log（前一日收盘价）

五日对数收盘价差＝log（当日收盘价）-log（五日前收盘价）

当日对数高低价差＝log（当日最高价）-log（当日最低价）

2010 年1月1日至2018年2月14日，螺纹钢期货主力合约的上诉五个技术指标的分布信息如下图所示：

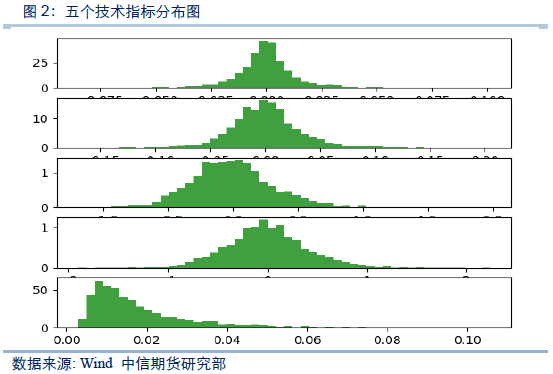
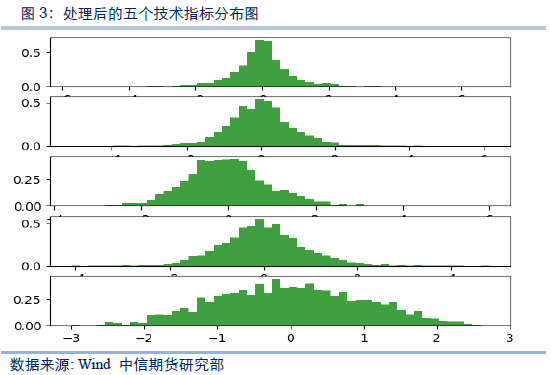
从上图中我们可以看到，最后一个可观察序列（当日对数高低价差）较为显著的偏离正态分布。因此对其进行Box-Cox Transformation数据转换方法，使其更接近正态分布。此外，在经验协方差矩阵计算过程中，具有较大方差的可观察序列将具有较大的权重。如果可观察序列的单位不同，其方差的差距可能达到数个数量级。这里为了保证所选的可观察序列具有接近的权重，我们对五个技术指标进行标准化（均值调整为0，标准差调整为1个单位）。经过以上处理后，可观察序列的分布如下图所示：

2.2 样本内数据分析

首先对样本内数据进行建模分析，输入的可观察序列为一日对数成交量差、五日对数成交量差、一日对数收盘价差、五日对数收盘价差以及当日对数高低价差等5个指标，隐藏状态数设置为7个，在出现每一个隐藏状态的第二天买入豆粕期货，分别分析各个隐藏状态的收益信息。

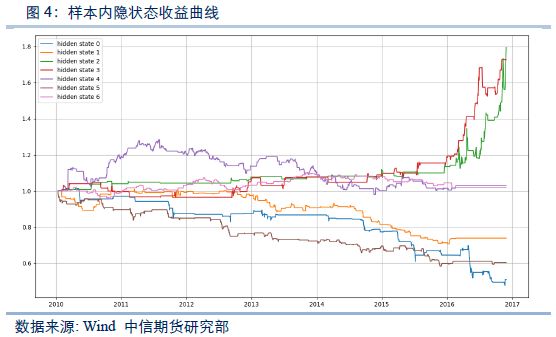
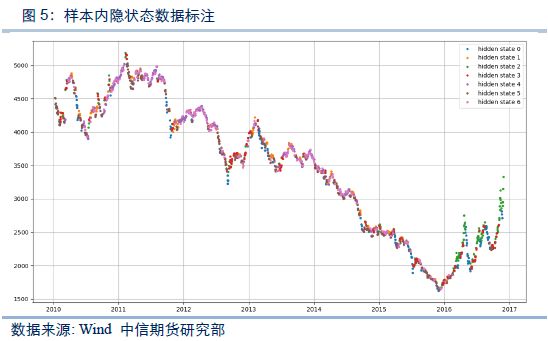
从上面两个图可以看到，在样本内数据时间段内，状态2和状态3为较明显的正收益隐状态，状态0，状态1和状态5为较明显的负收益隐状态，状态6和状态4为震荡隐状态。

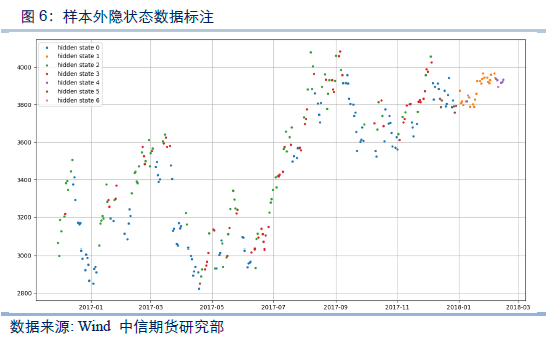
2.3 样本外数据分析

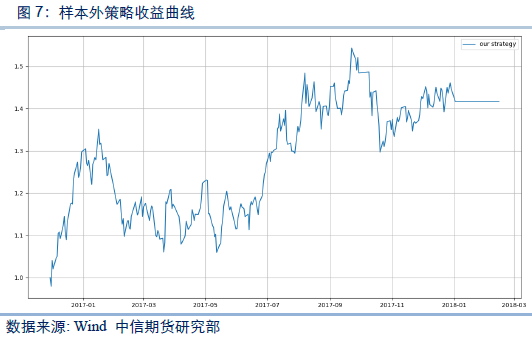
我们在接下来的分析中，利用同样的模型对样本外数据进行分析，同样是将样本内外的数据划分为7个不同的隐状态。通过样本内模型分析的结果，选择收益为正的隐状态2和隐状态3在第二天对螺纹钢期货开多头，选择收益为负的隐状态0，隐状态1和隐状态5在第二天对螺纹钢期货开空头。分析样本外时间段内的收益信息。

2.4 结论与后期优化方向 

将适当的技术指标纳入隐马尔可夫模型可观察向量组来预测螺纹钢期货的后期走势能取得一定的效果。但由于隐马尔可夫模型每次运行所得的隐状态分类较为随机，上升隐状态和下降隐状态是我们根据收益曲线人工区分的，模型的稳定性还有待提升。

目前我们只将一日对数成交量差、五日对数成交量差、一日对数收盘价差、五日对数收盘价差以及当日对数高低价差等5个指标纳入隐马尔可夫模型可观察向量组进行建模分析，没有考虑其他的一些技术指标。指标的选取范围较为狭窄。

在HMM模型的建立过程中并没有对模型的算法以及参数进行设置，只采用了初始的模型算法和参数，通过算法优化和参数设置可能得到更好的结果。

没有对不同隐状态对应的做多、做空操作进行分析，只是简单的选取了收益为正的隐状态做多，收益为负的隐状态做空。